Logistic regression predicts the probability of the outcome being true. In this exercise, we will implement a logistic regression and apply it to two different data sets. The file ex2data1.txt contains the dataset for the first part of the exercise and ex2data2.txt is data that we will use in the second part of the exercise. To learn the basics of Logistic Regression in R read this post.
In the first part of this exercise, we will build a logistic regression model to predict whether a student gets admitted into a university. Suppose that you are the administrator of a university department and you want to determine each applicant’s chance of admission based on their results on two exams. You have historical data from previous applicants that you can use as a training set for logistic regression. For each training example, you have the applicant’s scores on two exams and the admissions decision. Our task is to build a classification model that estimates an applicant’s probability of admission based the scores from those two exams.
library(ggplot2) library(data.table) library(magrittr)
Load the data and display first 6 observations
The first two columns contains the exam scores and the third column contains the label.
ex2data1 <- fread("ex2data1.txt",col.names=c("Exam1","Exam2","Label"))
head(ex2data1)
Exam1 Exam2 Label
34.62366 78.02469 0
30.28671 43.89500 0
35.84741 72.90220 0
60.18260 86.30855 1
79.03274 75.34438 1
45.08328 56.31637 0
Visualizing the data
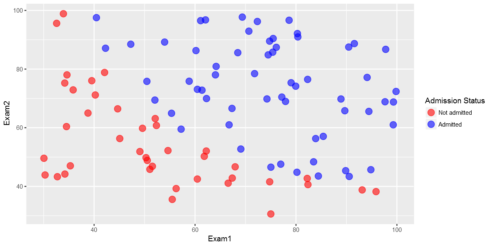
Before starting to implement any learning algorithm, it is always good to visualize the data if possible.
cols %ggplot(aes(x=Exam1,y=Exam2,color=factor(Label)))+geom_point(size = 4, shape = 19,alpha=0.6)+
scale_colour_manual(values = cols,labels = c("Not admitted", "Admitted"),name="Admission Status")
This is the formula:
Let’s code the sigmoid function so that we can call it in the rest of our programs.
my_sigmoid=function(z){
1/(1+exp(-z))
}For large positive values of x, the sigmoid should be close to 1, while for large negative values, the sigmoid should be close to 0. Evaluating sigmoid(0) should give exactly 0.5.
Let’s check!
my_sigmoid(0)0.5
my_sigmoid(10^10)1
my_sigmoid(-10^10)0
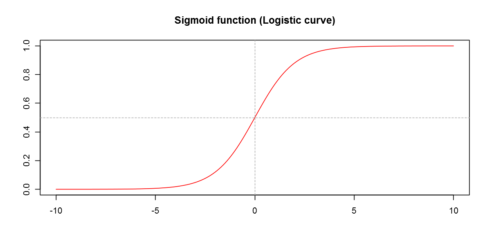
We can visualize the sigmoid function graphically:
x=seq(-10,10, by=0.1) y=my_sigmoid(x) plot(x,y,type="l",col="red",xlab="",ylab="",main="Sigmoid function (Logistic curve)") abline(v=0,lty = 2,col="gray 70") abline(h=0.5,lty = 2,col="gray70")
Cost function and gradient
This is the formula:
Add ones for the intercept term:
y=ex2data1$Label X=cbind(1,ex2data1$Exam1,ex2data1$Exam2) head(X) 1 34.62366 78.02469 1 30.28671 43.89500 1 35.84741 72.90220 1 60.18260 86.30855 1 79.03274 75.34438 1 45.08328 56.31637
Initialize fitting parameters:
initial_theta =matrix(rep(0,ncol(X)))
The function below calculates cost.
my_cost=function(theta, X, y){
cost_gradient=list()
h_theta= my_sigmoid(X%*%theta)
cost= 1/nrow(X)*sum(-y*log(h_theta)-(1-y)*log(1-h_theta))
return(cost)
}
What is the cost for the initial theta parameters, which are all zeros?
round(my_cost(initial_theta, X, y),3) 0.693
The function below calculates gradient.
my_gradient=function(theta, X, y){
h_theta= my_sigmoid(X%*%theta)
## OPTION 1-- looping
# gradient=rep(0,ncol(X))
# for(j in 1:ncol(X)){
# for(i in 1:nrow(X)){
# gradient[j]=gradient[j]+1/nrow(X)*(my_sigmoid(X[i,]%*%theta)-y[i])*X[i,j]
# }
# }
# option2-more succint
gradient= 1/nrow(X)*(my_sigmoid(t(theta)%*%t(X))-t(y))%*%X
return(gradient)
}
The gradient for the initial theta parameters, which are all zeros, is shown below
round(my_gradient(initial_theta, X, y),3) -0.1 -12.009 -11.263
General-purpose Optimization in lieu of Gradient Descent
We can use gradient descent to get the optimal theta values but using optimazation libraries converges quicker. So, let’s use the optim general-purpose Optimization in R to get the required theta values and the associated cost.
optimized=optim(par=initial_theta,X=X,y=y,fn=my_cost,gr=my_gradient) names(optimized) 'par' 'value' 'counts' 'convergence' 'message'
cat("The optimized theta values are: ")
round(optimized$par,3)
The optimized theta values are:
-25.165
0.206
0.202
cat('The cost at the final theta values is: ')
round(optimized$value,3)
The cost at the final theta values is:
0.203Decision Boundary
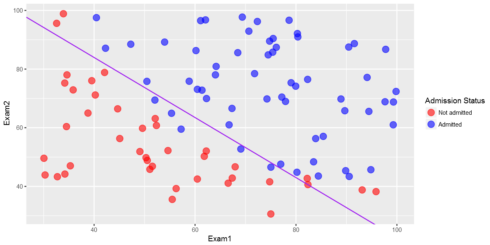
Now, let’s plot the decision boundary. Only 2 points are required to define a line, so let’s choose two endpoints.
plot_x = c(min(ex2data1$Exam1)-2,max(ex2data1$Exam1)+2)
# Calculate the decision boundary line
plot_y = (-1/optimized$par[3])*(optimized$par[2]*plot_x+optimized$par[1])
## Calculate slope and intercept
slope =(plot_y[2]-plot_y[1])/(plot_x[2]-plot_x[1])
intercept=plot_y[2]-slope*plot_x[2]
cols %ggplot(aes(x=Exam1,y=Exam2,color=factor(Label)))+geom_point(size = 4, shape = 19,alpha=0.6)+
scale_colour_manual(values = cols,labels = c("Not admitted", "Admitted"),name="Admission Status")+
geom_abline(intercept = intercept, slope = slope,col="purple",show.legend=TRUE)
Evaluating logistic regression
After learning the parameters, you can use the model to predict whether a particular student will be admitted. For example, for a student with an Exam 1 score of 45 and an Exam 2 score of 85, the probability of admission is shown below.
round(my_sigmoid(c(1,45,85)%*%optimized$par),3) 0.776
Model accuracy
Now, let’s calculate the model accuracy. Let’s use a threshould of 0.5.
ex2data1$fitted_result=my_sigmoid(X%*%optimized$par) ex2data1$fitted_result_label=ifelse(ex2data1$fitted_result>=0.5,1,0) head(ex2data1) Exam1 Exam2 Label fitted_result fitted_result_label 34.62366 78.02469 0 9.102720e-02 0 30.28671 43.89500 0 4.220398e-05 0 35.84741 72.90220 0 4.389943e-02 0 60.18260 86.30855 1 9.904316e-01 1 79.03274 75.34438 1 9.982001e-01 1 45.08328 56.31637 0 1.079133e-02 0
accuracy=sum(ex2data1$Label==ex2data1$fitted_result_label)/(nrow(ex2data1)) accuracy 0.89
Regularized logistic regression
In this part of the exercise, we will implement regularized logistic regression to predict whether microchips from a fabrication plant passes quality assurance (QA). During QA, each microchip goes through various tests to ensure it is functioning correctly. Suppose you are the product manager of the factory and you have the test results for some microchips on two different tests. From these two tests, you would like to determine whether the microchips should be accepted or rejected.
Visualizing the data
ex2data2 <- fread("ex2data2.txt",col.names=c("Test1","Test2","Label"))
head(ex2data2)
Test1 Test2 Label
0.051267 0.69956 1
-0.092742 0.68494 1
-0.213710 0.69225 1
-0.375000 0.50219 1
-0.513250 0.46564 1
-0.524770 0.20980 1
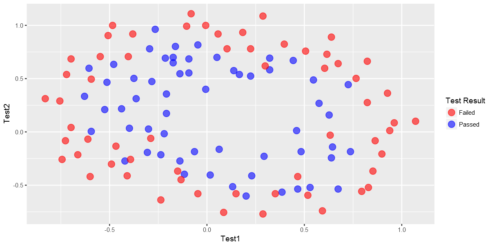
cols %ggplot(aes(x=Test1,y=Test2,color=factor(Label)))+geom_point(size = 4, shape = 19,alpha=0.6)+
scale_colour_manual(values = cols,labels = c("Failed", "Passed"),name="Test Result")
The above figure shows that our dataset cannot be separated into positive and negative examples by a straight-line through the plot. Therefore, a straightforward application of logistic regression will not perform well on this dataset since logistic regression will only be able to find a linear decision boundary.
Feature mapping
One way to fit the data better is to create more features from each data point. Let’s map the features into all polynomial terms of x1 and x2 up to the sixth power.
new_data=c()
for(i in 1:6){
for(j in 0:i){
temp= (ex2data2$Test1)^i+(ex2data2$Test2)^(i-j)
new_data=cbind(new_data,temp)
}
}
colnames(new_data)=paste0("V",1:ncol(new_data))
head(new_data)
V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 ... V18 V19 V20 V21 V22 V23 V24 V25 V26 V27
0.750827 1.051267 0.4920125 0.7021883 1.002628 0.34248835 0.48951894 0.69969475 1.0001347 0.23950380 ... 0.489384548 0.6995604 1.0000004 0.11720601 0.16754246 0.23949691 0.34235362 0.48938421 0.6995600 1.000000
0.592198 0.907258 0.4777439 0.6935411 1.008601 0.32053699 0.46834512 0.68414232 0.9992023 0.22016895 ... 0.469135943 0.6849331 0.9999931 0.10325661 0.15075249 0.22009561 0.32133531 0.46914344 0.6849406 1.000001
0.478540 0.786290 0.5248820 0.7379220 1.045672 0.32197261 0.46944951 0.68248944 0.9902394 0.23172821 ... 0.478764279 0.6918042 0.9995542 0.11014216 0.15906514 0.22973755 0.33182843 0.47930533 0.6923453 1.000095
0.127190 0.625000 0.3928198 0.6428150 1.140625 0.07391533 0.19946042 0.44945563 0.9472656 0.08337761 ... 0.244779025 0.4947742 0.9925842 0.01882106 0.03472131 0.06638313 0.12943062 0.25497571 0.5049709 1.002781
-0.047610 0.486750 0.4802462 0.7290656 1.263426 -0.03424282 0.08161744 0.33043683 0.8647968 0.11640420 ... 0.181204639 0.4300240 0.9643840 0.02847289 0.04017018 0.06529107 0.11924025 0.23510051 0.4839199 1.018280
-0.314970 0.475230 0.3193996 0.4851836 1.275384 -0.13527846 -0.10049699 0.06528697 0.8554870 0.07777351 ... 0.004219529 0.1700035 0.9602035 0.02096929 0.02129048 0.02282143 0.03011858 0.06490005 0.2306840 1.020884
y=ex2data2$Label X=new_data
As a result of this mapping, our vector of two features (the scores on two QA tests) has been transformed into a 28-dimensional vector. A logistic regression classifier trained on this higher-dimension feature vector will have a more complex decision boundary and will appear nonlinear when drawn in our 2-dimensional plot. While the feature mapping allows us to build a more expressive classifier, it also more susceptible to overfitting. In the next parts of the exercise, we will implement regularized logistic regression to fit the data and also see for ourselves how regularization can help combat the overfitting problem.
my_cost2=function(theta, X, y,lambda){
cost_gradient=list()
# cost_and_gradient compute cost and gradient for logistic regression using theta
h_theta= my_sigmoid(X%*%theta)
cost= 1/nrow(X)*sum(-y*log(h_theta)-(1-y)*log(1-h_theta))+lambda/(2*nrow(X))*sum(theta^2)
return(cost)
}
my_gradient2=function(theta, X, y,lambda){
h_theta= my_sigmoid(X%*%theta)
## OPTION 1-- looping
gradient=rep(0,ncol(X))
for(j in 2:ncol(X)){
for(i in 1:nrow(X)){
gradient[1]=gradient[1]+1/nrow(X)*(my_sigmoid(X[i,]%*%theta)-y[i])*X[i,1]
gradient[j]=gradient[j]+1/nrow(X)*(my_sigmoid(X[i,]%*%theta)-y[i])*X[i,j]+lambda/(nrow(X))*theta[j]
}
}
# option2-more succint
# gradient= 1/nrow(X)*(my_sigmoid(t(theta)%*%t(X))-t(y))%*%X+(lambda/(nrow(X)))*c(0,theta[-1])
return(gradient)
}Let’s initialize theta:
initial_theta =matrix(rep(0,ncol(X)))
What is the cost for the initial theta?
round(my_cost2(initial_theta,X,y,lambda=10),3) 0.693
Optimization
Now, since we have the cost function that we want to optimize and the gradient, we can use the optimization function optim to find the optimal theta values.
We have to try various values of lambda and select the best lambda based on cross-validation. But for now, let’s just take lambda=1.
optimized=optim(par=initial_theta,X=X,y=y,lambda=1,fn=my_cost2,gr=my_gradient2,method="BFGS")
The theta values from the optimization are shown below.
matrix(as.vector(optimized$par),ncol=9) 0.49507083 -0.05202124 -0.08527443 -0.1575100 -0.035020544 -0.11079198 0.01169745 -0.12174228 -0.12234383 0.05639364 -0.02062364 0.01959276 -0.1129876 -0.003622936 -0.06626957 0.04309506 -0.13996607 -0.01747664 -0.15688844 -0.05837426 0.05099037 -0.1398877 -0.092568188 -0.09316975 -0.14349836 -0.09544366 0.01392097
ex2data2$fitted_result=my_sigmoid(X%*%optimized$par)
Let’s use a threshold of 0.5.
ex2data2$fitted_result_label=ifelse(ex2data2$fitted_result>=0.5,1,0) head(ex2data2,10) Test1 Test2 Label fitted_result fitted_result_label 0.051267 0.699560 1 0.4765027 0 -0.092742 0.684940 1 0.4629791 0 -0.213710 0.692250 1 0.4410811 0 -0.375000 0.502190 1 0.4701446 0 -0.513250 0.465640 1 0.4459059 0 -0.524770 0.209800 1 0.4554844 0 -0.398040 0.034357 1 0.4730207 0 -0.305880 -0.192250 1 0.4618593 0 0.016705 -0.404240 1 0.4735035 0 0.131910 -0.513890 1 0.4640032 0
Evaluating the fit
Now, we can evaluate the fit by calculating various metrics such as F1 score, precision and recall. Let’s just see accuracy here. You can see the values of the other metrics here.
accuracy=sum(ex2data2$Label==ex2data2$fitted_result_label)/nrow(ex2data2)
cat("The accuracy is: ")
round(accuracy,3)
The accuracy is:
0.653 Summary
Logistic regression is a classification machine learning technique. In this blog post, we saw how to implement logistic regression with and without regularization. In the first part, we used it to predict if a student will be admitted to a university and in the second part, we used it to predict whether microchips from a fabrication plant pass quality assurance. We used special optimization function in lieu of gradient descent to get the optimal values of the coefficients. The data sets are from the Coursera machine learning course offered by Andrew Ng. The course is offered with Matlab/Octave. I am doing the exercises in that course with R. You can get the code from this Github repository.