Logistic regression is a method for fitting a regression curve, y = f(x), when y is a categorical variable. The typical use of this model is predicting y given a set of predictors x. The predictors can be continuous, categorical or a mix of both.
The categorical variable y, in general, can assume different values. In the simplest case scenario y is binary meaning that it can assume either the value 1 or 0. A classical example used in machine learning is email classification: given a set of attributes for each email such as a number of words, links, and pictures, the algorithm should decide whether the email is spam (1) or not (0). In this post, we call the model “binomial logistic regression”, since the variable to predict is binary, however, logistic regression can also be used to predict a dependent variable which can assume more than 2 values. In this second case, we call the model “multinomial logistic regression”. A typical example, for instance, would be classifying films between “Entertaining”, “borderline” or “boring”.
Logistic regression implementation in R
R makes it very easy to fit a logistic regression model. The function to be called is glm() and the fitting process is not so different from the one used in linear regression. In this post, I am going to fit a binary logistic regression model and explain each step.
The dataset
We’ll be working on the Titanic dataset. There are different versions of this dataset freely available online, however, I suggest to use the one available at Kaggle since it is almost ready to be used (in order to download it you need to sign up to Kaggle).
The dataset (training) is a collection of data about some of the passengers (889 to be precise), and the goal of the competition is to predict the survival (either 1 if the passenger survived or 0 if they did not) based on some features such as the class of service, the sex, the age etc. As you can see, we are going to use both categorical and continuous variables.
The data cleaning process
When working with a real dataset we need to take into account the fact that some data might be missing or corrupted, therefore we need to prepare the dataset for our analysis. As a first step we load the csv data using the read.csv() function.
Make sure that the parameter na.strings is equal to c("") so that each missing value is coded as a NA. This will help us in the next steps.
training.data.raw <- read.csv('train.csv',header=T,na.strings=c(""))
Now we need to check for missing values and look how many unique values there are for each variable using the sapply() function which applies the function passed as argument to each column of the dataframe.
sapply(training.data.raw,function(x) sum(is.na(x)))
sapply(training.data.raw, function(x) length(unique(x)))
PassengerId Survived Pclass Name Sex
0 0 0 0 0
Age SibSp Parch Ticket Fare
177 0 0 0 0
Cabin Embarked
687 2
PassengerId Survived Pclass Name Sex
891 2 3 891 2
Age SibSp Parch Ticket Fare
89 7 7 681 248
Cabin Embarked
148 4
A visual take on the missing values might be helpful: the Amelia package has a special plotting function missmap() that will plot your dataset and highlight missing values:
library(Amelia) missmap(training.data.raw, main = "Missing values vs observed")
The variable cabin has too many missing values, we will not use it. We will also drop PassengerId since it is only an index and Ticket.
Using the subset() function we subset the original dataset selecting the relevant columns only.
data <- subset(training.data.raw,select=c(2,3,5,6,7,8,10,12))
Taking care of the missing values
Now we need to account for the other missing values. R can easily deal with them when fitting a generalized linear model by setting a parameter inside the fitting function. However, personally, I prefer to replace the NAs “by hand” when is possible. There are different ways to do this, a typical approach is to replace the missing values with the average, the median or the mode of the existing one. I’ll be using the average.
data$Age[is.na(data$Age)] <- mean(data$Age,na.rm=T)
As far as categorical variables are concerned, using the read.table() or read.csv() by default will encode the categorical variables as factors. A factor is how R deals categorical variables.
We can check the encoding using the following lines of code
is.factor(data$Sex) is.factor(data$Embarked) TRUE TRUE
For a better understanding of how R is going to deal with the categorical variables, we can use the contrasts() function. This function will show us how the variables have been dummyfied by R and how to interpret them in a model.
contrasts(data$Sex)
contrasts(data$Embarked)
male
female 0
male 1
Q S
C 0 0
Q 1 0
S 0 1
For instance, you can see that in the variable sex, the female will be used as the reference. As for the missing values in Embarked, since there are only two, we will discard those two rows (we could also have replaced the missing values with the mode and keep the data points).
data <- data[!is.na(data$Embarked),] rownames(data) <- NULL
Before proceeding to the fitting process, let me remind you how important is cleaning and formatting of the data. This preprocessing step often is crucial for obtaining a good fit of the model and better predictive ability.
Model fitting
We split the data into two chunks: training and testing set. The training set will be used to fit our model which we will be testing over the testing set.
train <- data[1:800,] test <- data[801:889,]
Now, let’s fit the model. Be sure to specify the parameter family=binomial in the glm() function.
model <- glm(Survived ~.,family=binomial(link='logit'),data=train)
By using function summary() we obtain the results of our model:
summary(model)
Call:
glm(formula = Survived ~ ., family = binomial(link = "logit"),
data = train)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.6064 -0.5954 -0.4254 0.6220 2.4165
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 5.137627 0.594998 8.635 < 2e-16 ***
Pclass -1.087156 0.151168 -7.192 6.40e-13 ***
Sexmale -2.756819 0.212026 -13.002 < 2e-16 ***
Age -0.037267 0.008195 -4.547 5.43e-06 ***
SibSp -0.292920 0.114642 -2.555 0.0106 *
Parch -0.116576 0.128127 -0.910 0.3629
Fare 0.001528 0.002353 0.649 0.5160
EmbarkedQ -0.002656 0.400882 -0.007 0.9947
EmbarkedS -0.318786 0.252960 -1.260 0.2076
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1065.39 on 799 degrees of freedom
Residual deviance: 709.39 on 791 degrees of freedom
AIC: 727.39
Number of Fisher Scoring iterations: 5
Interpreting the results of our logistic regression model
Now we can analyze the fitting and interpret what the model is telling us.
First of all, we can see that SibSp, Fare and Embarked are not statistically significant. As for the statistically significant variables, sex has the lowest p-value suggesting a strong association of the sex of the passenger with the probability of having survived. The negative coefficient for this predictor suggests that all other variables being equal, the male passenger is less likely to have survived. Remember that in the logit model the response variable is log odds: ln(odds) = ln(p/(1-p)) = a*x1 + b*x2 + … + z*xn. Since male is a dummy variable, being male reduces the log odds by 2.75 while a unit increase in age reduces the log odds by 0.037.
Now we can run the anova() function on the model to analyze the table of deviance
anova(model, test="Chisq")
Analysis of Deviance Table
Model: binomial, link: logit
Response: Survived
Terms added sequentially (first to last)
Df Deviance Resid. Df Resid. Dev Pr(>Chi)
NULL 799 1065.39
Pclass 1 83.607 798 981.79 < 2.2e-16 ***
Sex 1 240.014 797 741.77 < 2.2e-16 ***
Age 1 17.495 796 724.28 2.881e-05 ***
SibSp 1 10.842 795 713.43 0.000992 ***
Parch 1 0.863 794 712.57 0.352873
Fare 1 0.994 793 711.58 0.318717
Embarked 2 2.187 791 709.39 0.334990
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
The difference between the null deviance and the residual deviance shows how our model is doing against the null model (a model with only the intercept). The wider this gap, the better. Analyzing the table we can see the drop in deviance when adding each variable one at a time. Again, adding Pclass, Sex and Age significantly reduces the residual deviance. The other variables seem to improve the model less even though SibSp has a low p-value. A large p-value here indicates that the model without the variable explains more or less the same amount of variation. Ultimately what you would like to see is a significant drop in deviance and the AIC.
While no exact equivalent to the R2 of linear regression exists, the McFadden R2 index can be used to assess the model fit.
library(pscl)
pR2(model)
llh llhNull G2 McFadden r2ML r2CU
-354.6950111 -532.6961008 356.0021794 0.3341513 0.3591775 0.4880244
Assessing the predictive ability of the model
In the steps above, we briefly evaluated the fitting of the model, now we would like to see how the model is doing when predicting y on a new set of data. By setting the parameter type='response', R will output probabilities in the form of P(y=1|X). Our decision boundary will be 0.5. If P(y=1|X) > 0.5 then y = 1 otherwise y=0. Note that for some applications different decision boundaries could be a better option.
fitted.results <- predict(model,newdata=subset(test,select=c(2,3,4,5,6,7,8)),type='response')
fitted.results <- ifelse(fitted.results > 0.5,1,0)
misClasificError <- mean(fitted.results != test$Survived)
print(paste('Accuracy',1-misClasificError))
"Accuracy 0.842696629213483"
The 0.84 accuracy on the test set is quite a good result. However, keep in mind that this result is somewhat dependent on the manual split of the data that I made earlier, therefore if you wish for a more precise score, you would be better off running some kind of cross validation such as k-fold cross validation.
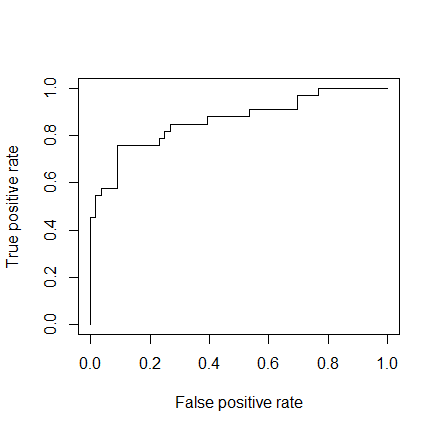
As a last step, we are going to plot the ROC curve and calculate the AUC (area under the curve) which are typical performance measurements for a binary classifier.
The ROC is a curve generated by plotting the true positive rate (TPR) against the false positive rate (FPR) at various threshold settings while the AUC is the area under the ROC curve. As a rule of thumb, a model with good predictive ability should have an AUC closer to 1 (1 is ideal) than to 0.5.
library(ROCR) p <- predict(model, newdata=subset(test,select=c(2,3,4,5,6,7,8)), type="response") pr <- prediction(p, test$Survived) prf <- performance(pr, measure = "tpr", x.measure = "fpr") plot(prf) auc <- performance(pr, measure = "auc") auc <- [email protected][[1]] auc 0.8647186
I hope this post will be useful. A gist with the full code for this example can be found here.
Thank you for reading this post, leave a comment below if you have any question.