Use Box Plots to Assess the Distribution and to Identify the Outliers in Your Dataset

After you check the distribution of the data by plotting the histogram, the second thing to do is to look for outliers. Identifying the outliers is important because it might happen that an association you find in your analysis can be explained by the presence of outliers.

The best tool to identify the outliers is the box plot. Through box plots, we find the minimum, lower quartile (25th percentile), median (50th percentile), upper quartile (75th percentile), and a maximum of an continues variable. The function to build a boxplot is boxplot().

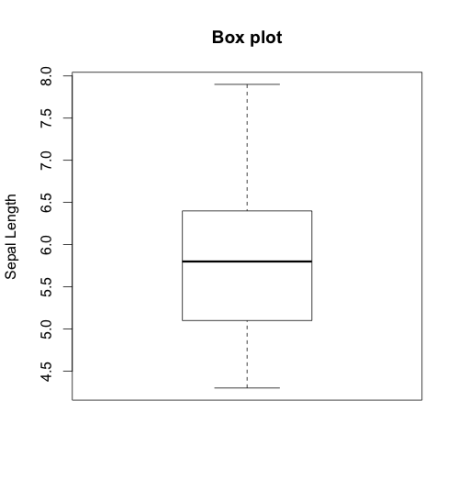
Let build the following boxplot with iris dataset which is preloaded with R:

boxplot(iris$Sepal.Length, main="Box plot", ylab="Sepal Length")

This will generate the following box plot. Each horizontal line starting from bottom will show the minimum, lower quartile, median, upper quartile and maximum value of Sepal.Length.

We can use a box plot to explore the distribution of a continues variable across the strata. I’m saying strata because the variable should be categorical. For example, you want to see what is the distribution of age among individuals with and without blood pressure. In the example below, I’m showing the length of sepal in different species.

# build the box plot
boxplot(Sepal.Length ~ Species, data=iris,
     main="Box Plot",
     xlab="Species",
     ylab="Sepal Length")

This will generate the following boxplots:

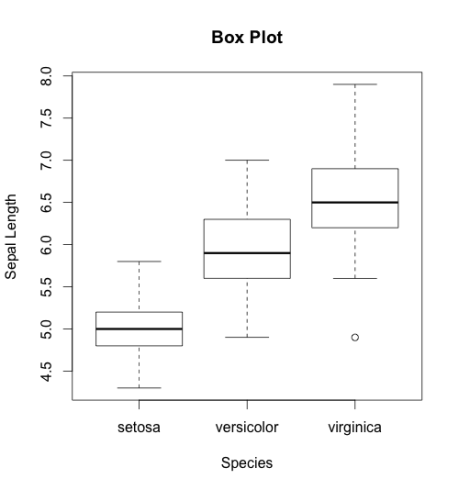
If you look at the bottom of third box plot you will find an outlier. If you find in your dataset an outlier I suggest to remove it. Although, to remove an outlier should be a topic of another post, for now, you can check your dataset and manually remove the observation. However, there are functions which remove outliers automatically.

Feel free to post comments if you have any question.

Box plots