In the previous part of this tutorial, we build several models based on logistic regression. One aspect to be further considered is the decision threshold tuning that may help in reaching a better accuracy. We are going to show a procedure able to determine an optimal value for such purpose. ROC plots will be introduced as well.
Decision Threshold Tuning
As default, caret uses 0.5 as threshold decision value to be used as probability cutoff value. We are going to show how to tune such decision threshold to achieve a better training set accuracy. We then compare how the testing set accuracy changes accordingly.
Tuning Analysis
We load previously saved training, testing datasets together with the models we have already determined.
suppressPackageStartupMessages(library(caret)) suppressPackageStartupMessages(library(ROCR)) set.seed(1023) readRDS(file="wf_log_reg_part2.rds") Copy
The following tuning procedure explores a pool of cutoff values giving back a table reporting {cutoff, accuracy, specificity} triplets. Its inspection allows to identify the cutoff value providing with the highest accuracy. In case of a tie in accuracy value, we choose the lowest cutoff value of such.
glm.tune <- function(glm_model, dataset) {
results <- data.frame()
for (q in seq(0.2, 0.8, by = 0.02)) {
fitted_values <- glm_model$finalModel$fitted.values
prediction <- as.factor(ifelse(fitted_values >= q, "Yes", "No"))
cm <- confusionMatrix(prediction, dataset$RainTomorrow)
accuracy <- cm$overall["Accuracy"]
specificity <- cm$byClass["Specificity"]
results <- rbind(results, data.frame(cutoff=q, accuracy=accuracy, specificity = specificity))
}
rownames(results) <- NULL
results
}
Copy
In the utility function above, we included also the specificity metrics. Specificity is defined as TN/(TN+FP) and in the next part of this series we will discuss some aspects of. Let us show an example of confusion matrix with some metrics computation to clarify the terminology.
Reference
Prediction No Yes
No 203 42
Yes 0 3
Accuracy : 0.8306 = (TP+TN)/(TP+TN+FP+FN) = (203+3)/(203+3+42+0)
Sensitivity : 1.00000 = TP/(TP+FN) = 203/(203+0)
Specificity : 0.06667 = TN/(TN+FP) = 3/(3+42)
Pos Pred Value : 0.82857 = TP/(TP+FP) = 203/(203+42)
Neg Pred Value : 1.00000 = TN/(TN+FN) = 3/(3+0)
Copy
Please note that the “No” column is associated to a positive outcome, whilst “Yes” to a negative one. Specificity measure how good we are in predict that {RainTomorrow = “No”} and actually it is and this is something that we are going to investigate in next post of this series.
The logistic regression models to be tuned are:
mod9am_c1_fit: RainTomorrow ~ Cloud9am + Humidity9am + Pressure9am + Temp9am mod3pm_c1_fit: RainTomorrow ~ Cloud3pm + Humidity3pm + Pressure3pm + Temp3pm mod_ev_c2_fit: RainTomorrow ~ Cloud3pm + Humidity3pm + Pressure3pm + Temp3pm + WindGustDir mod_ev_c3_fit: RainTomorrow ~ Pressure3pm + Sunshine Copy
In the following analysis, for all models we determine the cutoff value providing with the highest accuracy.
glm.tune(mod9am_c1_fit, training) cutoff accuracy specificity 1 0.20 0.7822581 0.73333333 2 0.22 0.7862903 0.71111111 3 0.24 0.7943548 0.68888889 4 0.26 0.8064516 0.64444444 5 0.28 0.8104839 0.64444444 6 0.30 0.8145161 0.60000000 7 0.32 0.8185484 0.57777778 8 0.34 0.8185484 0.51111111 9 0.36 0.8104839 0.46666667 10 0.38 0.8266129 0.46666667 11 0.40 0.8266129 0.40000000 12 0.42 0.8306452 0.40000000 13 0.44 0.8266129 0.37777778 14 0.46 0.8346774 0.35555556 15 0.48 0.8467742 0.33333333 16 0.50 0.8508065 0.31111111 17 0.52 0.8427419 0.26666667 18 0.54 0.8467742 0.26666667 19 0.56 0.8346774 0.20000000 20 0.58 0.8387097 0.20000000 21 0.60 0.8387097 0.20000000 22 0.62 0.8346774 0.17777778 23 0.64 0.8387097 0.17777778 24 0.66 0.8346774 0.15555556 25 0.68 0.8387097 0.15555556 26 0.70 0.8387097 0.13333333 27 0.72 0.8387097 0.13333333 28 0.74 0.8346774 0.11111111 29 0.76 0.8266129 0.06666667 30 0.78 0.8266129 0.06666667 31 0.80 0.8306452 0.06666667 Copy
The optimal cutoff value is equal to 0.5. In this case, we find the same cutoff value as the default the caret package takes advantage of for logistic regression models.
opt_cutoff <- 0.5
pred_test <- predict(mod9am_c1_fit, testing, type = "prob")
prediction = as.factor(ifelse(pred_test$Yes >= opt_cutoff, "Yes", "No"))
confusionMatrix(prediction, testing$RainTomorrow)
Confusion Matrix and Statistics
Reference
Prediction No Yes
No 80 12
Yes 6 7
Accuracy : 0.8286
95% CI : (0.7427, 0.8951)
No Information Rate : 0.819
P-Value [Acc > NIR] : 0.4602
Kappa : 0.3405
Mcnemar's Test P-Value : 0.2386
Sensitivity : 0.9302
Specificity : 0.3684
Pos Pred Value : 0.8696
Neg Pred Value : 0.5385
Prevalence : 0.8190
Detection Rate : 0.7619
Detection Prevalence : 0.8762
Balanced Accuracy : 0.6493
'Positive' Class : No
Copy
Then, tuning the 3PM model.
glm.tune(mod3pm_c1_fit, training) cutoff accuracy specificity 1 0.20 0.8064516 0.7777778 2 0.22 0.8185484 0.7555556 3 0.24 0.8225806 0.7333333 4 0.26 0.8306452 0.6888889 5 0.28 0.8467742 0.6666667 6 0.30 0.8467742 0.6444444 7 0.32 0.8427419 0.6222222 8 0.34 0.8669355 0.6222222 9 0.36 0.8709677 0.6222222 10 0.38 0.8629032 0.5777778 11 0.40 0.8669355 0.5777778 12 0.42 0.8669355 0.5555556 13 0.44 0.8548387 0.4666667 14 0.46 0.8548387 0.4444444 15 0.48 0.8588710 0.4444444 16 0.50 0.8669355 0.4444444 17 0.52 0.8629032 0.4222222 18 0.54 0.8669355 0.4222222 19 0.56 0.8669355 0.3777778 20 0.58 0.8669355 0.3777778 21 0.60 0.8588710 0.3333333 22 0.62 0.8548387 0.3111111 23 0.64 0.8508065 0.2888889 24 0.66 0.8467742 0.2666667 25 0.68 0.8387097 0.2222222 26 0.70 0.8387097 0.2222222 27 0.72 0.8346774 0.2000000 28 0.74 0.8387097 0.1777778 29 0.76 0.8346774 0.1555556 30 0.78 0.8346774 0.1555556 31 0.80 0.8306452 0.1111111 Copy
The optimal cutoff value is equal to 0.36.
opt_cutoff <- 0.36
pred_test <- predict(mod3pm_c1_fit, testing, type="prob")
prediction = as.factor(ifelse(pred_test$Yes >= opt_cutoff, "Yes", "No"))
confusionMatrix(prediction, testing$RainTomorrow)
Confusion Matrix and Statistics
Reference
Prediction No Yes
No 81 5
Yes 5 14
Accuracy : 0.9048
95% CI : (0.8318, 0.9534)
No Information Rate : 0.819
P-Value [Acc > NIR] : 0.0112
Kappa : 0.6787
Mcnemar's Test P-Value : 1.0000
Sensitivity : 0.9419
Specificity : 0.7368
Pos Pred Value : 0.9419
Neg Pred Value : 0.7368
Prevalence : 0.8190
Detection Rate : 0.7714
Detection Prevalence : 0.8190
Balanced Accuracy : 0.8394
'Positive' Class : No
Copy
We improved the test accuracy, previously resulting as equal to 0.8857 and now equal to 0.9048 (please take a look at part #2 of this tutorial to know about the test accuracy with 0.5 cutoff value). Then, the first evening hours model.
glm.tune(mod_ev_c2_fit, training) cutoff accuracy specificity 1 0.20 0.8387097 0.8444444 2 0.22 0.8467742 0.8222222 3 0.24 0.8548387 0.8222222 4 0.26 0.8629032 0.8000000 5 0.28 0.8588710 0.7333333 6 0.30 0.8709677 0.7333333 7 0.32 0.8790323 0.7111111 8 0.34 0.8830645 0.6888889 9 0.36 0.8870968 0.6666667 10 0.38 0.8870968 0.6666667 11 0.40 0.8951613 0.6666667 12 0.42 0.8991935 0.6666667 13 0.44 0.8991935 0.6666667 14 0.46 0.8951613 0.6444444 15 0.48 0.8951613 0.6222222 16 0.50 0.8951613 0.6222222 17 0.52 0.8951613 0.6000000 18 0.54 0.8911290 0.5777778 19 0.56 0.8911290 0.5777778 20 0.58 0.8951613 0.5777778 21 0.60 0.8911290 0.5555556 22 0.62 0.8870968 0.5111111 23 0.64 0.8830645 0.4888889 24 0.66 0.8830645 0.4666667 25 0.68 0.8790323 0.4222222 26 0.70 0.8709677 0.3555556 27 0.72 0.8548387 0.2666667 28 0.74 0.8508065 0.2444444 29 0.76 0.8427419 0.1777778 30 0.78 0.8387097 0.1555556 31 0.80 0.8387097 0.1555556 Copy
The optimal cutoff value is equal to 0.42.
opt_cutoff <- 0.42
pred_test <- predict(mod_ev_c2_fit, testing, type="prob")
prediction = as.factor(ifelse(pred_test$Yes >= opt_cutoff, "Yes", "No"))
confusionMatrix(prediction, testing$RainTomorrow)
Confusion Matrix and Statistics
Reference
Prediction No Yes
No 82 8
Yes 4 11
Accuracy : 0.8857
95% CI : (0.8089, 0.9395)
No Information Rate : 0.819
P-Value [Acc > NIR] : 0.04408
Kappa : 0.58
Mcnemar's Test P-Value : 0.38648
Sensitivity : 0.9535
Specificity : 0.5789
Pos Pred Value : 0.9111
Neg Pred Value : 0.7333
Prevalence : 0.8190
Detection Rate : 0.7810
Detection Prevalence : 0.8571
Balanced Accuracy : 0.7662
'Positive' Class : No
Copy
We did not improve the accuracy as the default cutoff value provides with the same. Other metrics changed and in particular we notice that the sensitivity decreased a little bit while the positive predicted value improved. Then the second evening hours model.
glm.tune(mod_ev_c3_fit, training) cutoff accuracy specificity 1 0.20 0.8225806 0.8000000 2 0.22 0.8145161 0.7333333 3 0.24 0.8064516 0.6666667 4 0.26 0.8145161 0.6666667 5 0.28 0.8145161 0.6222222 6 0.30 0.8185484 0.6222222 7 0.32 0.8266129 0.6000000 8 0.34 0.8185484 0.5555556 9 0.36 0.8306452 0.5333333 10 0.38 0.8467742 0.5333333 11 0.40 0.8467742 0.5111111 12 0.42 0.8427419 0.4666667 13 0.44 0.8508065 0.4666667 14 0.46 0.8467742 0.4222222 15 0.48 0.8467742 0.4000000 16 0.50 0.8508065 0.4000000 17 0.52 0.8548387 0.4000000 18 0.54 0.8508065 0.3777778 19 0.56 0.8669355 0.3777778 20 0.58 0.8669355 0.3555556 21 0.60 0.8629032 0.3333333 22 0.62 0.8588710 0.3111111 23 0.64 0.8548387 0.2888889 24 0.66 0.8508065 0.2666667 25 0.68 0.8467742 0.2444444 26 0.70 0.8387097 0.2000000 27 0.72 0.8387097 0.1777778 28 0.74 0.8346774 0.1555556 29 0.76 0.8306452 0.1333333 30 0.78 0.8306452 0.1333333 31 0.80 0.8306452 0.1333333 Copy
The optimal cutoff value is equal to 0.56.
opt_cutoff <- 0.56
pred_test <- predict(mod_ev_c3_fit, testing, type="prob")
prediction = as.factor(ifelse(pred_test$Yes >= opt_cutoff, "Yes", "No")
confusionMatrix(prediction, testing$RainTomorrow)
Confusion Matrix and Statistics
Reference
Prediction No Yes
No 82 8
Yes 4 11
Accuracy : 0.8857
95% CI : (0.8089, 0.9395)
No Information Rate : 0.819
P-Value [Acc > NIR] : 0.04408
Kappa : 0.58
Mcnemar's Test P-Value : 0.38648
Sensitivity : 0.9535
Specificity : 0.5789
Pos Pred Value : 0.9111
Neg Pred Value : 0.7333
Prevalence : 0.8190
Detection Rate : 0.7810
Detection Prevalence : 0.8571
Balanced Accuracy : 0.7662
'Positive' Class : No
Copy
In this case, we did not improved the accuracy of this model. Other metrics changed and in particular we notice that the sensitivity is slightly higher than the default cutoff driven value (0.9419), and the positive predicted value decreased a little bit (for default cutoff was 0.9205).
ROC analysis
To have a visual understanding of the classification performances and compute further metrics, we are going to take advantage of the ROCr package facilities. We plot ROC curves and determine the corresponding AUC value. That is going to be done for each model. The function used to accomplish with this task is the following.
glm.perf.plot <- function (prediction, cutoff) {
perf <- performance(prediction, measure = "tpr", x.measure = "fpr")
par(mfrow=(c(1,2)))
plot(perf, col="red")
grid()
perf <- performance(prediction, measure = "acc", x.measure = "cutoff")
plot(perf, col="red")
abline(v = cutoff, col="green")
grid()
auc_res <- performance(prediction, "auc")
auc_res@y.values[[1]]
}
Copy
In the following, each model will be considered, AUC value printed out and ROC plots given.
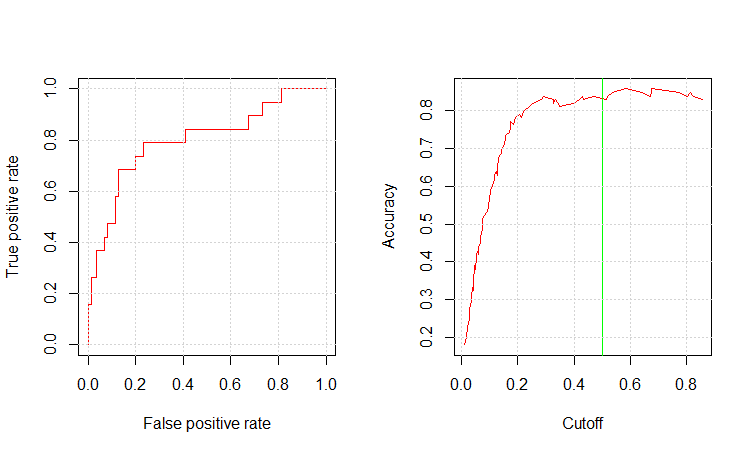
mod9am_pred_prob <- predict(mod9am_c1_fit, testing, type="prob") mod9am_pred_resp <- prediction(mod9am_pred_prob$Yes, testing$RainTomorrow) glm.perf.plot(mod9am_pred_resp, 0.5) [1] 0.8004896 Copy
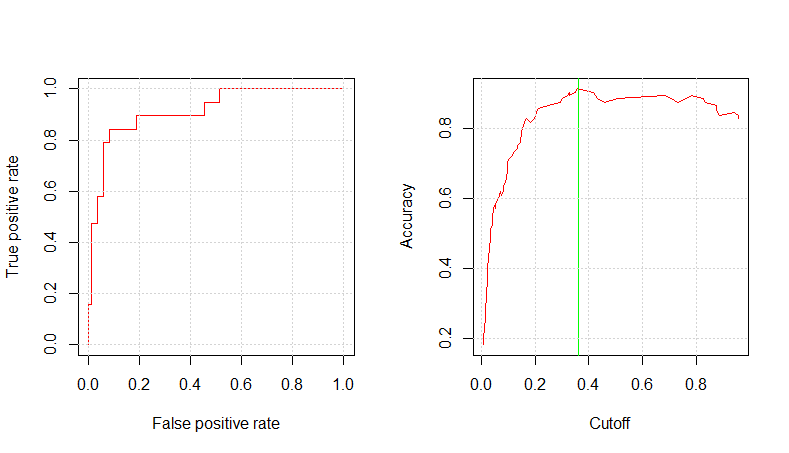
mod3pm_pred_prob <- predict(mod3pm_c1_fit, testing, type="prob") mod3pm_pred_resp <- prediction(mod3pm_pred_prob$Yes, testing$RainTomorrow) glm.perf.plot(mod3pm_pred_resp, 0.36) [1] 0.9155447 Copy
The 3PM model shows the highest AUC value among all the models.
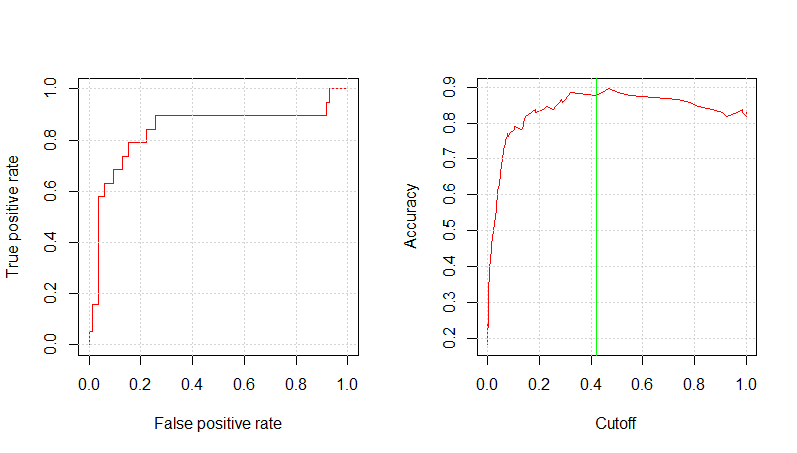
mod_ev_c2_prob <- predict(mod_ev_c2_fit, testing, type="prob") mod_ev_c2_pred_resp <- prediction(mod_ev_c2_prob$Yes , testing$RainTomorrow) glm.perf.plot(mod_ev_c2_pred_resp, 0.42) [1] 0.8390453 Copy
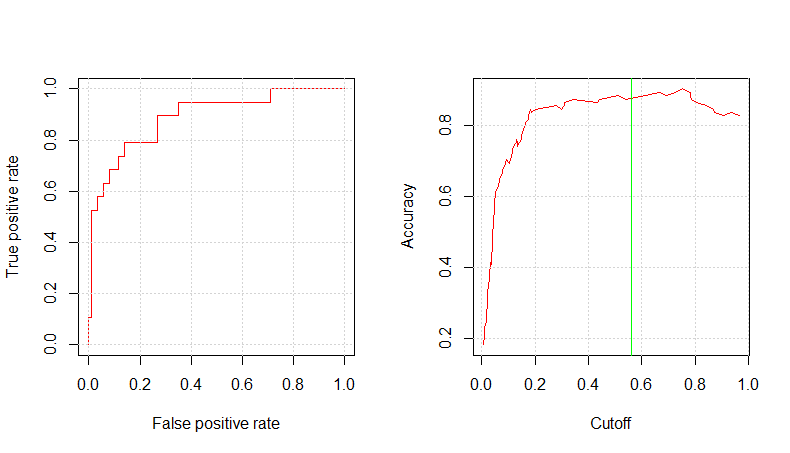
mod_ev_c3_prob <- predict(mod_ev_c3_fit, testing, type="prob") mod_ev_c3_pred_resp <- prediction(mod_ev_c3_prob$Yes, testing$RainTomorrow) glm.perf.plot(mod_ev_c3_pred_resp, 0.56) [1] 0.8886169 Copy
Conclusions
By tuning the decision threshold, we were able to improve training and testing set accuracy. It turned out the 3PM model achieved a satisfactory accuracy. ROC plots gave us an understanding of how true/false positive rates vary and what is the accuracy obtained by a specific decision threshold value (i.e. cutoff value). Ultimately, AUC values were reported.
If you have any questions, please feel free to comment below.