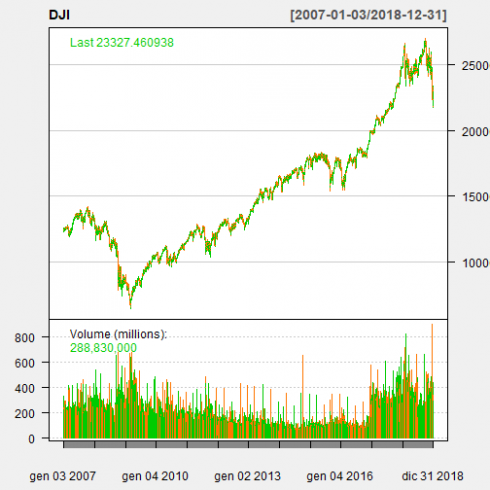
In this four-post series, I am going to analyze the Dow Jones Industrial Average (DJIA) index on years 2007-2018. The Dow Jones Industrial Average (DIJA) is a stock market index that indicates the value of thirty large, publicly owned companies based in the United States. The value of the DJIA is based upon the sum of the price of one share of stock for each component company. The sum is corrected by a factor which changes whenever one of the component stocks has a stock split or stock dividend. See ref. [1] for further details.
The main questions I will try to answer are:
- How the returns and trade volume have changed over the years?
- How the returns and trade volume volatility have changed over the years?
- How can we model the returns volatility?
- How can we model the trade volume volatility?
For the purpose, this post series is split as follows:
Part 1: getting data, summaries, and plots of daily and weekly log-returns
Part 2: getting data, summaries, and plots of daily trade volume and its log-ratio
Part 3: daily log-returns analysis and GARCH model definition
Part 4: daily trade volume analysis and GARCH model definition
Packages
The packages being used in this post series are herein listed.
suppressPackageStartupMessages(library(lubridate)) # dates manipulation
suppressPackageStartupMessages(library(fBasics)) # enhanced summary statistics
suppressPackageStartupMessages(library(lmtest)) # coefficients significance tests
suppressPackageStartupMessages(library(urca)) # unit rooit test
suppressPackageStartupMessages(library(ggplot2)) # visualization
suppressPackageStartupMessages(library(quantmod)) # getting financial data
suppressPackageStartupMessages(library(PerformanceAnalytics)) # calculating returns
suppressPackageStartupMessages(library(rugarch)) # GARCH modeling
suppressPackageStartupMessages(library(FinTS)) # ARCH test
suppressPackageStartupMessages(library(forecast)) # ARMA modeling
suppressPackageStartupMessages(library(strucchange)) # structural changes
suppressPackageStartupMessages(library(TSA)) # ARMA order identification
CopyTo the right, I added a short comment to highlight the main functionalities I took advantage from. Of course, those packages offer much more than just what I indicated.
Packages version are herein listed.
packages <- c("lubridate", "fBasics", "lmtest", "urca", "ggplot2", "quantmod", "PerformanceAnalytics", "rugarch", "FinTS", "forecast", "strucchange", "TSA")
version <- lapply(packages, packageVersion)
version_c <- do.call(c, version)
data.frame(packages=packages, version = as.character(version_c))
## packages version
## 1 lubridate 1.7.4
## 2 fBasics 3042.89
## 3 lmtest 0.9.36
## 4 urca 1.3.0
## 5 ggplot2 3.1.0
## 6 quantmod 0.4.13
## 7 PerformanceAnalytics 1.5.2
## 8 rugarch 1.4.0
## 9 FinTS 0.4.5
## 10 forecast 8.4
## 11 strucchange 1.5.1
## 12 TSA 1.2
CopyThe R language version running on Windows-10 is:
R.version
>## _
## platform x86_64-w64-mingw32
## arch x86_64
## os mingw32
## system x86_64, mingw32
## status
## major 3
## minor 5.2
## year 2018
## month 12
## day 20
## svn rev 75870
## language R
## version.string R version 3.5.2 (2018-12-20)
## nickname Eggshell Igloo
CopyGetting Data
Taking advantage of the getSymbols() function made available within quantmod package we get Dow Jones Industrial Average from 2007 up to the end of 2018.
suppressMessages(getSymbols("^DJI", from = "2007-01-01", to = "2019-01-01"))
## [1] "DJI"
Copydim(DJI)
## [1] 3020 6
Copyclass(DJI)
## [1] "xts" "zoo"
CopyLet us have a look at the DJI xts object which provides six-time series, as we can see.
head(DJI)
## DJI.Open DJI.High DJI.Low DJI.Close DJI.Volume DJI.Adjusted
## 2007-01-03 12459.54 12580.35 12404.82 12474.52 327200000 12474.52
## 2007-01-04 12473.16 12510.41 12403.86 12480.69 259060000 12480.69
## 2007-01-05 12480.05 12480.13 12365.41 12398.01 235220000 12398.01
## 2007-01-08 12392.01 12445.92 12337.37 12423.49 223500000 12423.49
## 2007-01-09 12424.77 12466.43 12369.17 12416.60 225190000 12416.60
## 2007-01-10 12417.00 12451.61 12355.63 12442.16 226570000 12442.16
Copytail(DJI)
## DJI.Open DJI.High DJI.Low DJI.Close DJI.Volume DJI.Adjusted
## 2018-12-21 22871.74 23254.59 22396.34 22445.37 900510000 22445.37
## 2018-12-24 22317.28 22339.87 21792.20 21792.20 308420000 21792.20
## 2018-12-26 21857.73 22878.92 21712.53 22878.45 433080000 22878.45
## 2018-12-27 22629.06 23138.89 22267.42 23138.82 407940000 23138.82
## 2018-12-28 23213.61 23381.88 22981.33 23062.40 336510000 23062.40
## 2018-12-31 23153.94 23333.18 23118.30 23327.46 288830000 23327.46
CopyMore precisely, we have available OHLC (Open, High, Low, Close) index value, adjusted close value and trade volume. Here we can see the corresponding chart as produced by the chartSeries within the quantmod package.
chartSeries(DJI, type = "bars", theme="white")
CopyWe herein analyse the adjusted close value.
dj_close <- DJI[,"DJI.Adjusted"]
CopySimple and log returns
Simple returns are defined as:
Rt := PtPt−1 − 1
Log returns are defined as:
rt := lnPtPt−1 = ln(1+Rt)
See ref. [4] for further details.
We compute log returns by taking advantage of CalculateReturns within PerformanceAnalytics package.
dj_ret <- CalculateReturns(dj_close, method = "log")
dj_ret <- na.omit(dj_ret)
CopyLet us have a look.
head(dj_ret)
## DJI.Adjusted
## 2007-01-04 0.0004945580
## 2007-01-05 -0.0066467273
## 2007-01-08 0.0020530973
## 2007-01-09 -0.0005547987
## 2007-01-10 0.0020564627
## 2007-01-11 0.0058356461
Copytail(dj_ret)
## DJI.Adjusted
## 2018-12-21 -0.018286825
## 2018-12-24 -0.029532247
## 2018-12-26 0.048643314
## 2018-12-27 0.011316355
## 2018-12-28 -0.003308137
## 2018-12-31 0.011427645
CopyThis gives the following plot.
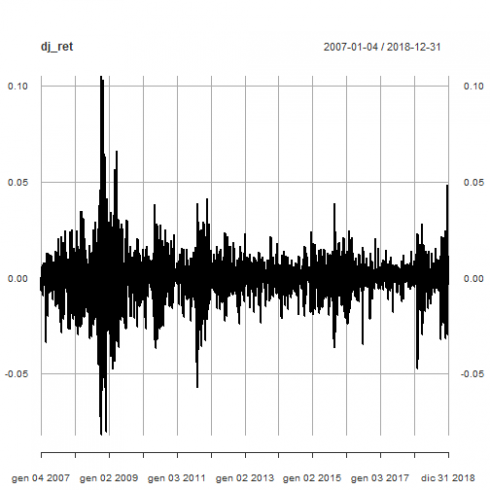
plot(dj_ret)
CopySharp increases and decreases in volatility can be eye-balled. That will be in-depth verified in part 3.
Helper Functions
We need some helper functions to ease some basic data conversion, summaries and plots. Here below the details.
1. Conversion from xts to dataframe with year and value column. That allows for summarizations and plots on year basis.
xts_to_dataframe <- function(data_xts) {
df_t <- data.frame(year = factor(year(index(data_xts))), value = coredata(data_xts))
colnames(df_t) <- c( "year", "value")
df_t
}
Copy2. Enhanced summaries statistics for data stored as data frame columns.
bs_rn <- rownames(basicStats(rnorm(10,0,1))) # gathering the basic stats dataframe output row names that get lost with tapply()
dataframe_basicstats <- function(dataset) {
result <- with(dataset, tapply(value, year, basicStats))
df_result <- do.call(cbind, result)
rownames(df_result) <- bs_rn
as.data.frame(df_result)
}
Copy3. Basic statistics dataframe row threshold filtering to return the associated column names.
filter_dj_stats <- function(dataset_basicstats, metricname, threshold) {
r <- which(rownames(dataset_basicstats) == metricname)
colnames(dataset_basicstats[r, which(dataset_basicstats[r,] > threshold), drop = FALSE])
}
Copy4. Box-plots with faceting based on years.
dataframe_boxplot <- function(dataset, title) {
p <- ggplot(data = dataset, aes(x = year, y = value)) + theme_bw() + theme(legend.position = "none") + geom_boxplot(fill = "lightblue")
p <- p + theme(axis.text.x = element_text(angle = 90, hjust = 1)) + ggtitle(title) + ylab("year")
p
}
Copy5. Density plots with faceting based on years.
dataframe_densityplot <- function(dataset, title) {
p <- ggplot(data = dataset, aes(x = value)) + geom_density(fill = "lightblue")
p <- p + facet_wrap(. ~ year)
p <- p + theme_bw() + theme(legend.position = "none") + ggtitle(title)
p
}
Copy6. QQ plots with faceting based on years.
dataframe_qqplot <- function(dataset, title) {
p <- ggplot(data = dataset, aes(sample = value)) + stat_qq(colour = "blue") + stat_qq_line()
p <- p + facet_wrap(. ~ year)
p <- p + theme_bw() + theme(legend.position = "none") + ggtitle(title)
p
}
Copy7. Shapiro Test
shp_pvalue <- function (v) {
shapiro.test(v)$p.value
}
dataframe_shapirotest <- function(dataset) {
result <- with(dataset, tapply(value, year, shp_pvalue))
as.data.frame(result)
}
CopyDaily Log-returns Exploratory Analysis
We transform our original Dow Jones time series into a dataframe with year and value columns. That will ease plots and summaries by year.
dj_ret_df <- xts_to_dataframe(dj_ret)
head(dj_ret_df)
## year value
## 1 2007 0.0004945580
## 2 2007 -0.0066467273
## 3 2007 0.0020530973
## 4 2007 -0.0005547987
## 5 2007 0.0020564627
## 6 2007 0.0058356461
Copytail(dj_ret_df)
## year value
## 3014 2018 -0.018286825
## 3015 2018 -0.029532247
## 3016 2018 0.048643314
## 3017 2018 0.011316355
## 3018 2018 -0.003308137
## 3019 2018 0.011427645
CopyBasic statistics summary
Basic statistics summary is given.
(dj_stats <- dataframe_basicstats(dj_ret_df))
## 2007 2008 2009 2010 2011
## nobs 250.000000 253.000000 252.000000 252.000000 252.000000
## NAs 0.000000 0.000000 0.000000 0.000000 0.000000
## Minimum -0.033488 -0.082005 -0.047286 -0.036700 -0.057061
## Maximum 0.025223 0.105083 0.066116 0.038247 0.041533
## 1. Quartile -0.003802 -0.012993 -0.006897 -0.003853 -0.006193
## 3. Quartile 0.005230 0.007843 0.008248 0.004457 0.006531
## Mean 0.000246 -0.001633 0.000684 0.000415 0.000214
## Median 0.001098 -0.000890 0.001082 0.000681 0.000941
## Sum 0.061427 -0.413050 0.172434 0.104565 0.053810
## SE Mean 0.000582 0.001497 0.000960 0.000641 0.000837
## LCL Mean -0.000900 -0.004580 -0.001207 -0.000848 -0.001434
## UCL Mean 0.001391 0.001315 0.002575 0.001678 0.001861
## Variance 0.000085 0.000567 0.000232 0.000104 0.000176
## Stdev 0.009197 0.023808 0.015242 0.010182 0.013283
## Skewness -0.613828 0.224042 0.070840 -0.174816 -0.526083
## Kurtosis 1.525069 3.670796 2.074240 2.055407 2.453822
## 2012 2013 2014 2015 2016
## nobs 250.000000 252.000000 252.000000 252.000000 252.000000
## NAs 0.000000 0.000000 0.000000 0.000000 0.000000
## Minimum -0.023910 -0.023695 -0.020988 -0.036402 -0.034473
## Maximum 0.023376 0.023263 0.023982 0.038755 0.024384
## 1. Quartile -0.003896 -0.002812 -0.002621 -0.005283 -0.002845
## 3. Quartile 0.004924 0.004750 0.004230 0.005801 0.004311
## Mean 0.000280 0.000933 0.000288 -0.000090 0.000500
## Median -0.000122 0.001158 0.000728 -0.000211 0.000738
## Sum 0.070054 0.235068 0.072498 -0.022586 0.125884
## SE Mean 0.000470 0.000403 0.000432 0.000613 0.000501
## LCL Mean -0.000645 0.000139 -0.000564 -0.001298 -0.000487
## UCL Mean 0.001206 0.001727 0.001139 0.001118 0.001486
## Variance 0.000055 0.000041 0.000047 0.000095 0.000063
## Stdev 0.007429 0.006399 0.006861 0.009738 0.007951
## Skewness 0.027235 -0.199407 -0.332766 -0.127788 -0.449311
## Kurtosis 0.842890 1.275821 1.073234 1.394268 2.079671
## 2017 2018
## nobs 251.000000 251.000000
## NAs 0.000000 0.000000
## Minimum -0.017930 -0.047143
## Maximum 0.014468 0.048643
## 1. Quartile -0.001404 -0.005017
## 3. Quartile 0.003054 0.005895
## Mean 0.000892 -0.000231
## Median 0.000655 0.000695
## Sum 0.223790 -0.057950
## SE Mean 0.000263 0.000714
## LCL Mean 0.000373 -0.001637
## UCL Mean 0.001410 0.001175
## Variance 0.000017 0.000128
## Stdev 0.004172 0.011313
## Skewness -0.189808 -0.522618
## Kurtosis 2.244076 2.802996
CopyIn the following, we make specific comments to some relevant aboveshown metrics.
Mean
Years when Dow Jones daily log-returns have positive mean values are:
filter_dj_stats(dj_stats, "Mean", 0)
## [1] "2007" "2009" "2010" "2011" "2012" "2013" "2014" "2016" "2017"
CopyAll Dow Jones daily log-returns mean values in ascending order.
dj_stats["Mean",order(dj_stats["Mean",,])]
## 2008 2018 2015 2011 2007 2012 2014
## Mean -0.001633 -0.000231 -9e-05 0.000214 0.000246 0.00028 0.000288
## 2010 2016 2009 2017 2013
## Mean 0.000415 5e-04 0.000684 0.000892 0.000933
CopyMedian
Years when Dow Jones daily log-returns have positive median are:
filter_dj_stats(dj_stats, "Median", 0)
## [1] "2007" "2009" "2010" "2011" "2013" "2014" "2016" "2017" "2018"
CopyAll Dow Jones daily log-returns median values in ascending order.
dj_stats["Median",order(dj_stats["Median",,])]
## 2008 2015 2012 2017 2010 2018 2014
## Median -0.00089 -0.000211 -0.000122 0.000655 0.000681 0.000695 0.000728
## 2016 2011 2009 2007 2013
## Median 0.000738 0.000941 0.001082 0.001098 0.001158
CopySkewness
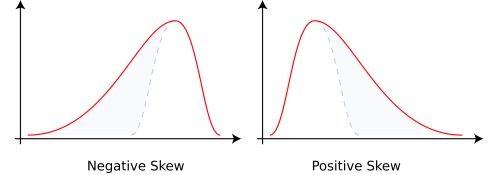
A spatial distribution has positive skewness when it has tendency to produce more positive extreme values above rather than negative ones. Negative skew commonly indicates that the tail is on the left side of the distribution, and positive skew indicates that the tail is on the right. Here is a sample picture to explain.
Years when Dow Jones daily log-returns have positive skewness are:
filter_dj_stats(dj_stats, "Skewness", 0)
## [1] "2008" "2009" "2012"
CopyAll Dow Jones daily log-returns skewness values in ascending order.
dj_stats["Skewness",order(dj_stats["Skewness",,])]
## 2007 2011 2018 2016 2014 2013
## Skewness -0.613828 -0.526083 -0.522618 -0.449311 -0.332766 -0.199407
## 2017 2010 2015 2012 2009 2008
## Skewness -0.189808 -0.174816 -0.127788 0.027235 0.07084 0.224042
CopyExcess Kurtosis
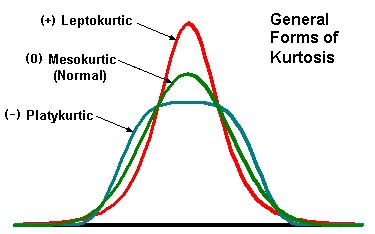
The Kurtosis is a measure of the “tailedness” of the probability distribution of a real-valued random variable. The kurtosis of any univariate normal distribution is 3. The excess kurtosis is equal to the kurtosis minus 3 and eases the comparison to the normal distribution. The basicStats function within the fBasics package reports the excess kurtosis. Here is a sample picture to explain.
Years when Dow Jones daily log-returns have positive excess kurtosis are:
filter_dj_stats(dj_stats, "Kurtosis", 0)
## [1] "2007" "2008" "2009" "2010" "2011" "2012" "2013" "2014" "2015" "2016"
## [11] "2017" "2018"
CopyAll Dow Jones daily log-returns excess kurtosis values in ascending order.
dj_stats["Kurtosis",order(dj_stats["Kurtosis",,])]
## 2012 2014 2013 2015 2007 2010 2009
## Kurtosis 0.84289 1.073234 1.275821 1.394268 1.525069 2.055407 2.07424
## 2016 2017 2011 2018 2008
## Kurtosis 2.079671 2.244076 2.453822 2.802996 3.670796
CopyYear 2018 has the closest excess kurtosis to 2008.
Box-plots
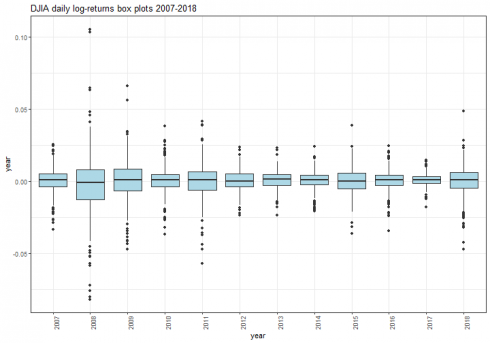
dataframe_boxplot(dj_ret_df, "DJIA daily log-returns box plots 2007-2018")
CopyWe can see how the most extreme values occurred on 2008. Starting on 2009, the values range gets narrow, with the exception of 2011 and 2015. However, comparing 2017 with 2018, it is remarkable an improved tendency to produce more extreme values on last year.
Density plots
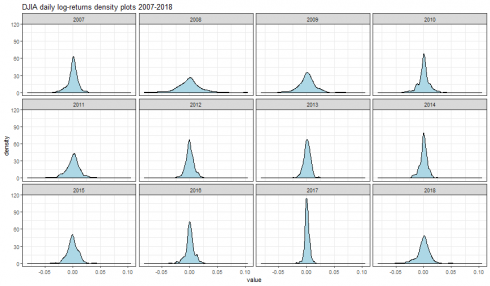
dataframe_densityplot(dj_ret_df, "DJIA daily log-returns density plots 2007-2018")
CopyYear 2007 has remarkable negative skewness. Year 2008 is characterized by flatness and extreme values. The 2017 peakness is in constrant with the flatness and left skeweness of 2018 results.
Shapiro Tests
dataframe_shapirotest(dj_ret_df)
## result
## 2007 5.989576e-07
## 2008 5.782666e-09
## 2009 1.827967e-05
## 2010 3.897345e-07
## 2011 5.494349e-07
## 2012 1.790685e-02
## 2013 8.102500e-03
## 2014 1.750036e-04
## 2015 5.531137e-03
## 2016 1.511435e-06
## 2017 3.304529e-05
## 2018 1.216327e-07
CopyThe null hypothesis of normality is rejected for all years 2007-2018.
QQ plots
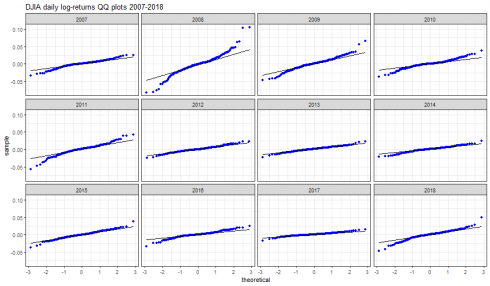
dataframe_qqplot(dj_ret_df, "DJIA daily log-returns QQ plots 2007-2018")
CopyStrong departure from normality of daily log returns (and hence log-normality for discrete returns) is visible on years 2008, 2009, 2010, 2011 and 2018.
Weekly Log-returns Exploratory Analysis
The weekly log returns can be computed starting from the daily ones. Let us suppose to analyse the trading week on days {t-4, t-3, t-2, t-1, t} and to know closing price at day t-5 (last day of the previous week). We define the weekly log-return as:
rwt := lnPtPt−5
That can be rewritten as:
rwt = lnPtPt−1Pt−2Pt−3Pt−4Pt−1Pt−2Pt−3Pt−4Pt−5== lnPtPt−1+lnPt−1Pt−2+lnPt−2Pt−3+lnPt−3Pt−4 + lnPt−4Pt−5 ==rt+rt−1+rt−2+rt−3+rt−4
Hence the weekly log return is the sum of daily log returns applied to the trading week window.
We take a look at Dow Jones weekly log-returns.
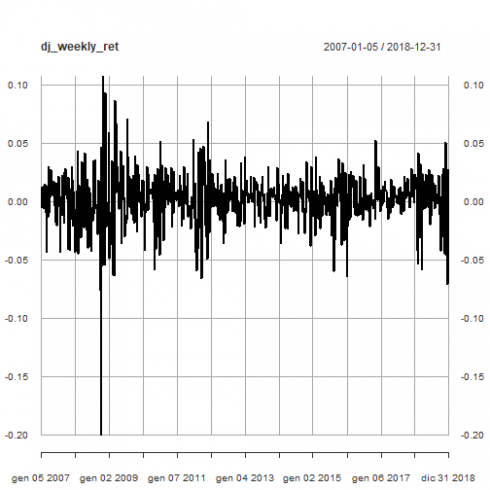
dj_weekly_ret <- apply.weekly(dj_ret, sum)
plot(dj_weekly_ret)
CopyThat plot shows sharp increses and decreases of volatility.
We transform the original time series data and index into a dataframe.
dj_weekly_ret_df <- xts_to_dataframe(dj_weekly_ret)
dim(dj_weekly_ret_df)
## [1] 627 2
Copyhead(dj_weekly_ret_df)
## year value
## 1 2007 -0.0061521694
## 2 2007 0.0126690596
## 3 2007 0.0007523559
## 4 2007 -0.0062677053
## 5 2007 0.0132434177
## 6 2007 -0.0057588519
Copytail(dj_weekly_ret_df)
## year value
## 622 2018 0.05028763
## 623 2018 -0.04605546
## 624 2018 -0.01189714
## 625 2018 -0.07114867
## 626 2018 0.02711928
## 627 2018 0.01142764
CopyBasic statistics summary
(dj_stats <- dataframe_basicstats(dj_weekly_ret_df))
## 2007 2008 2009 2010 2011 2012
## nobs 52.000000 52.000000 53.000000 52.000000 52.000000 52.000000
## NAs 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000
## Minimum -0.043199 -0.200298 -0.063736 -0.058755 -0.066235 -0.035829
## Maximum 0.030143 0.106977 0.086263 0.051463 0.067788 0.035316
## 1. Quartile -0.009638 -0.031765 -0.015911 -0.007761 -0.015485 -0.010096
## 3. Quartile 0.014808 0.012682 0.022115 0.016971 0.014309 0.011887
## Mean 0.001327 -0.008669 0.003823 0.002011 0.001035 0.001102
## Median 0.004244 -0.006811 0.004633 0.004529 0.001757 0.001166
## Sum 0.069016 -0.450811 0.202605 0.104565 0.053810 0.057303
## SE Mean 0.002613 0.006164 0.004454 0.003031 0.003836 0.002133
## LCL Mean -0.003919 -0.021043 -0.005115 -0.004074 -0.006666 -0.003181
## UCL Mean 0.006573 0.003704 0.012760 0.008096 0.008736 0.005384
## Variance 0.000355 0.001975 0.001051 0.000478 0.000765 0.000237
## Stdev 0.018843 0.044446 0.032424 0.021856 0.027662 0.015382
## Skewness -0.680573 -0.985740 0.121331 -0.601407 -0.076579 -0.027302
## Kurtosis -0.085887 5.446623 -0.033398 0.357708 0.052429 -0.461228
## 2013 2014 2015 2016 2017 2018
## nobs 52.000000 52.000000 53.000000 52.000000 52.000000 53.000000
## NAs 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000
## Minimum -0.022556 -0.038482 -0.059991 -0.063897 -0.015317 -0.071149
## Maximum 0.037702 0.034224 0.037693 0.052243 0.028192 0.050288
## 1. Quartile -0.001738 -0.006378 -0.012141 -0.007746 -0.002251 -0.011897
## 3. Quartile 0.011432 0.010244 0.009620 0.012791 0.009891 0.019857
## Mean 0.004651 0.001756 -0.000669 0.002421 0.004304 -0.001093
## Median 0.006360 0.003961 0.000954 0.001947 0.004080 0.001546
## Sum 0.241874 0.091300 -0.035444 0.125884 0.223790 -0.057950
## SE Mean 0.001828 0.002151 0.002609 0.002436 0.001232 0.003592
## LCL Mean 0.000981 -0.002563 -0.005904 -0.002470 0.001830 -0.008302
## UCL Mean 0.008322 0.006075 0.004567 0.007312 0.006778 0.006115
## Variance 0.000174 0.000241 0.000361 0.000309 0.000079 0.000684
## Stdev 0.013185 0.015514 0.018995 0.017568 0.008886 0.026154
## Skewness -0.035175 -0.534403 -0.494963 -0.467158 0.266281 -0.658951
## Kurtosis -0.200282 0.282354 0.665460 2.908942 -0.124341 -0.000870
CopyIn the following, we make specific comments to some relevant aboveshown metrics.
Mean
Years when Dow Jones weekly log-returns have positive mean are:
filter_dj_stats(dj_stats, "Mean", 0)
## [1] "2007" "2009" "2010" "2011" "2012" "2013" "2014" "2016" "2017"
CopyAll mean values in ascending order.
dj_stats["Mean",order(dj_stats["Mean",,])]
## 2008 2018 2015 2011 2012 2007 2014
## Mean -0.008669 -0.001093 -0.000669 0.001035 0.001102 0.001327 0.001756
## 2010 2016 2009 2017 2013
## Mean 0.002011 0.002421 0.003823 0.004304 0.004651
CopyMedian
Years when Dow Jones weekly log-returns have positive median are:
filter_dj_stats(dj_stats, "Median", 0)
## [1] "2007" "2009" "2010" "2011" "2012" "2013" "2014" "2015" "2016" "2017"
## [11] "2018"
CopyAll median values in ascending order.
dj_stats["Median",order(dj_stats["Median",,])]
## 2008 2015 2012 2018 2011 2016 2014
## Median -0.006811 0.000954 0.001166 0.001546 0.001757 0.001947 0.003961
## 2017 2007 2010 2009 2013
## Median 0.00408 0.004244 0.004529 0.004633 0.00636
CopySkewness
Years when Dow Jones weekly log-returns have positive skewness are:
filter_dj_stats(dj_stats, "Skewness", 0)
## [1] "2009" "2017"
CopyAll skewness values in ascending order.
dj_stats["Skewness",order(dj_stats["Skewness",,])]
## 2008 2007 2018 2010 2014 2015
## Skewness -0.98574 -0.680573 -0.658951 -0.601407 -0.534403 -0.494963
## 2016 2011 2013 2012 2009 2017
## Skewness -0.467158 -0.076579 -0.035175 -0.027302 0.121331 0.266281
CopyExcess Kurtosis
Years when Dow Jones weekly log-returns have positive excess kurtosis are:
filter_dj_stats(dj_stats, "Kurtosis", 0)
## [1] "2008" "2010" "2011" "2014" "2015" "2016"
CopyAll excess kurtosis values in ascending order.
dj_stats["Kurtosis",order(dj_stats["Kurtosis",,])]
## 2012 2013 2017 2007 2009 2018
## Kurtosis -0.461228 -0.200282 -0.124341 -0.085887 -0.033398 -0.00087
## 2011 2014 2010 2015 2016 2008
## Kurtosis 0.052429 0.282354 0.357708 0.66546 2.908942 5.446623
CopyYear 2008 has also highest weekly kurtosis. However in this scenario, 2017 has negative kurtosis and year 2016 has the second highest kurtosis.
Box-plots
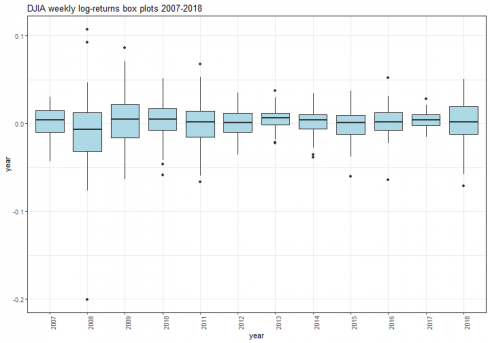
dataframe_boxplot(dj_weekly_ret_df, "DJIA weekly log-returns box plots 2007-2018")
CopyDensity plots
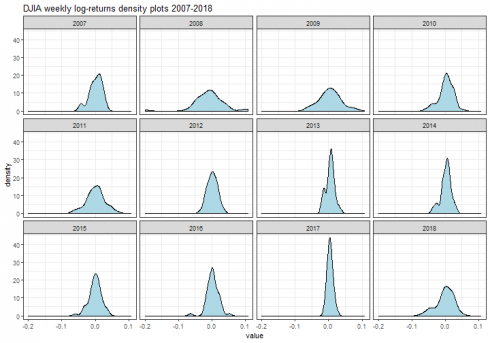
dataframe_densityplot(dj_weekly_ret_df, "DJIA weekly log-returns density plots 2007-2018")
CopyShapiro Tests
dataframe_shapirotest(dj_weekly_ret_df)
## result
## 2007 0.0140590311
## 2008 0.0001397267
## 2009 0.8701335006
## 2010 0.0927104389
## 2011 0.8650874270
## 2012 0.9934600084
## 2013 0.4849043121
## 2014 0.1123139646
## 2015 0.3141519756
## 2016 0.0115380989
## 2017 0.9465281164
## 2018 0.0475141869
CopyThe null hypothesis of normality is rejected for years 2007, 2008, 2016.
QQ plots
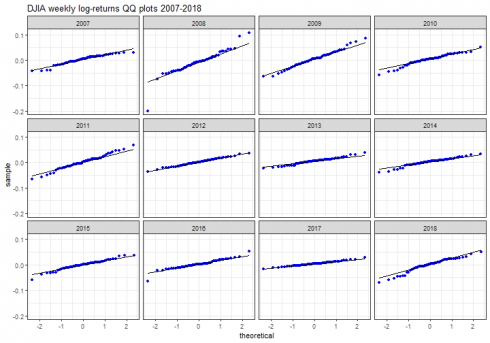
dataframe_qqplot(dj_weekly_ret_df, "DJIA weekly log-returns QQ plots 2007-2018")
CopyStrong departure from normality is particularly visible on year 2008.
Saving the current enviroment for further analysis.
save.image(file='DowEnvironment.RData')
CopyIf you have any questions, please feel free to comment below.
References
- Dow Jones Industrial Average
- Skewness
- Kurtosis
- An introduction to analysis of financial data with R, Wiley, Ruey S. Tsay
- Time series analysis and its applications, Springer ed., R.H. Shumway, D.S. Stoffer
- Applied Econometric Time Series, Wiley, W. Enders, 4th ed.]
- Forecasting – Principle and Practice, Texts, R.J. Hyndman
- Options, Futures and other Derivatives, Pearson ed., J.C. Hull
- An introduction to rugarch package
- Applied Econometrics with R, Achim Zeileis, Christian Kleiber – Springer Ed.
- GARCH modeling: diagnostic tests
Disclaimer
Any securities or databases referred in this post are solely for illustration purposes, and under no regard should the findings presented here be interpreted as investment advice or promotion of any particular security or source.