Today will be a brief introduction in to circular statistics (sometimes referred to as directional statistics). Circular statistics is an interesting subdivision of statistics involving observations taken as vectors around a unit circle. As an example, imagine measuring birth times at a hospital over a 24-hour cycle, or the directional dispersion of a group of migratory animals. This type of data is involved in a variety fields, such as ecology, climatology, and biochemistry. The nature of measuring observations around a unit circle necessitates a different approach to hypothesis testing. Distributions need to be “wrapped” around the circle to be of use, and conventional estimators such as the sample mean or sample variance hold no water.
In this post, we will conduct Rao’s Spacing Test to assess the uniformity of a circular dataset. This is a basic procedure and should be thought of as an introduction to handling circular data.
Getting started
We are going to conduct a hypothesis test on turtles, a small dataset consisting of the arrival angles of 10 green sea turtles to their nesting island. Our goal is to determine where the arrival angles show signs of directionality or are more indicative of a random scatter.
First, install the circular package and attach the turtles dataset.
install.packages("circular")
require(circular)
attach(turtles)
Plotting the data
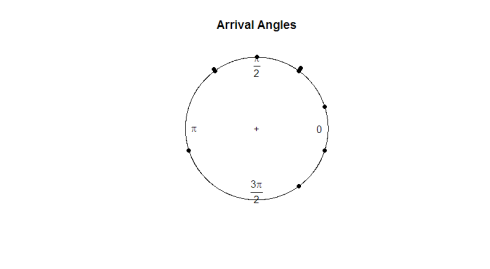
The circular package contains its own plotting function, plot.circular. Let’s observe the arrival angles of the turtles.
plot.circular(arrival)
Given the eye test, the observations appear to be uniform around the circle. If we want to run a hypothesis test to determine if the data is truly uniform, we will need to develop a test statistic that works with angular data.
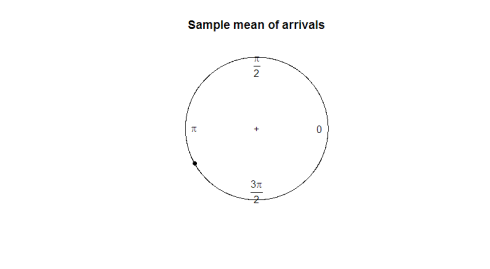
What is a good parameter for us to utilize? Taking the sample mean doesn’t tell us much about the direction of the data (180 degrees is not a useful mean of 2 degrees and 358 degrees). In the following plot, observe how the sample mean is of no use in representing the shape or spread of our data.
mean(arrival) plot.circular(mean(arrival)) [1] 0.9120794
Instead, we will use a method that determines directionality by measuring the average space between observations. This test is called Rao’s Spacing Test.
Rao’s Spacing Test
Rao’s Spacing Test was developed to assess the uniformity of circular data. It uses the space between observations to determine if the data shows significant directionality. If the data is uniform, observations should tend to be evenly spaced apart.
Here is the test statistic \(U\) for Rao’s Spacing Test: $$U = 1/2\sum\limits_{i=1}^n |T_{i} – λ| $$ where \(λ = 360/n, T_{i} = f_{i+1}-f_{i}\) and \(T_{n} = (360-f_{n})+f_{1}\)
Basically, the test statistic aggregates the deviations between consecutive points, each one weighted by the total number of observations in the dataset.
We will use the rao.spacing.test() function to run this hypotheses test. Our null hypothesis says the data is of a uniform distribution, while the alternate states the data shows signs of directionality. Let’s run the test.
rao.spacing.test(arrival,alpha=.10)
Rao's Spacing Test of Uniformity
Test Statistic = 127.2689
Level 0.1 critical value = 161.23
Do not reject null hypothesis of uniformity
With a test statistic of 127 falling below the critical value of 161, the data fails to significantly lean in any direction. We can not reject the hypothesis that the turtles arrivals are of a uniform distribution.
Conclusion
Rao’s spacing test determined the data to show no signs of directional trends. We cannot reject the null hypothesis of uniformity and will assume uniformity in regards to the direction of arrival. While this post was a relatively basic tutorial, many people in the data science community haven’t worked with circular data before. It is an interesting subtopic to dive in to as well as a young field of statistics that is still evolving.
Final remarks
I would like to extend credit to S. Rao Jammalamadaka PhD, of the University of California, Santa Barbara, and his textbook “Topics in Circular Statistics” for sparking my interest in the field of circular statistics.